Oleg's argument against call/cc links to one of his lesser known posts, Delimited continuations do dynamic-wind. In it he first shows how to implement yielding generators in terms of delimited control, and then shows how such generators lead to a natural definition of dynamic-wind, in userland, whereas with undelimited continuations, dynamic-wind has to be primitive.
(This is not entirely true. Kernel can implement dynamic-wind in userland, too, by means of its guarded undelimited continuations. And in Scheme 48, dynamic-wind is also implemented in userland with undelimited continuations, albeit in terms of a slightly lower level API than call/cc. Same is true for other Schemes, such as MIT Scheme. And probably the earliest definition of dynamic-wind, in Embedding Continuations in Procedural Objects is also in userland, so I'm a bit confused actually, as to why Oleg considers dynamic-wind primitive...)
Back to Oleg's generators in terms of delimited control. While one may argue against first-class continuations, whether delimited or not, I think having them in the language is great for quickly prototyping different ideas, such as generators. This has always been a forte of Lisp, and so high-powered control flow operations seem a good fit for the language, even if their runtime cost may be slightly higher than a more specialized, native implementation of some specific control feature, such as generators.
The basic ideas of generators are: you have a block of code, the generator, which may either normally return a value by means of reaching the end of the block, or it may intermittently yield a value. To call a generator, we need a boundary around it, so we wrap it in a prompt with reset. Yielding suspends the generator, capturing its delimited continuation up to the prompt, and delivers the value and this continuation to the caller, outside the boundary. Value and continuation are wrapped up in a special record type, so the caller can distinguish yields from an ordinary return, which doesn't wrap the value in any way (and neither provides a continuation for resuming, obviously). (This could probably be handled more elegantly with Racket's abort handlers.)
In this Gist, I've commented Oleg's implementation of generators and dynamic-wind.
I think it's a great example of how simple it is to add specific control flow features to a language with general (delimited) continuations.
Oh, and in typical Oleg style, the article then goes on about how you can implement call/cc in terms of generators, which makes his dynamic-wind compatible with existing Scheme examples using call/cc.
Showing posts with label continuations. Show all posts
Showing posts with label continuations. Show all posts
Saturday, August 11, 2012
Wednesday, August 1, 2012
Understanding metacontinuations for delimited control
Metacontinuations arise in some implementations of delimited control such as in A Monadic Framework for Delimited Continuations.
In addition to the usual continuation register K, an interpreter with metacontinuations has a metacontinuation register MK.
Initially, K points to an empty continuation KDone, and MK points to an empty metacontinuation MKDone:
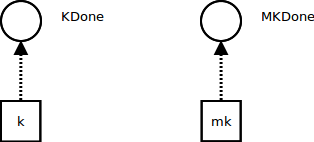
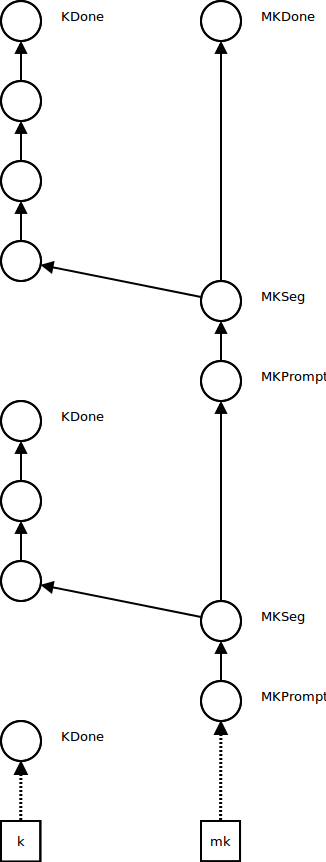
When the ordinary continuation reaches KDone, we look at the metacontinuation: if it's MKDone, the program is finished and we return its result. Otherwise, we underflow the metacontinuation by reestablishing the next continuation segment as the current continuation and the next metacontinuation as the current metacontinuation.
In addition to the usual continuation register K, an interpreter with metacontinuations has a metacontinuation register MK.
Initially, K points to an empty continuation KDone, and MK points to an empty metacontinuation MKDone:

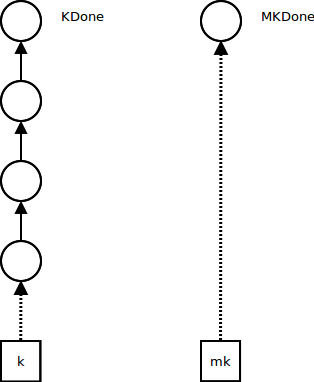
Ordinary computations influence only the continuation K - they push continuation frames while the metacontinuation MK stays the same:

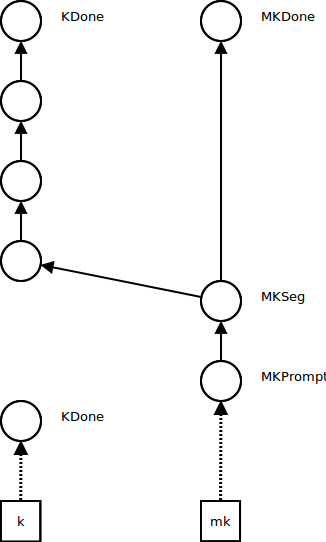
Control operations such as pushing a prompt (continuation delimiter) influence the metacontinuation. A segment metacontinuation frame MKSeg stores the continuation segment at which the control effect occurred and a pointer to the next metacontinuation. A prompt metacontinuation frame MKPrompt remembers the prompt and points to the segment frame (the reason for splitting this operation into two metacontinuation frames is that it makes the code simpler; see the paper). MK now points to the prompt metaframe, and K points to a new empty continuation KDone:

Further non-control computations occur in the new continuation, while the metacontinuation stays the same, as before:

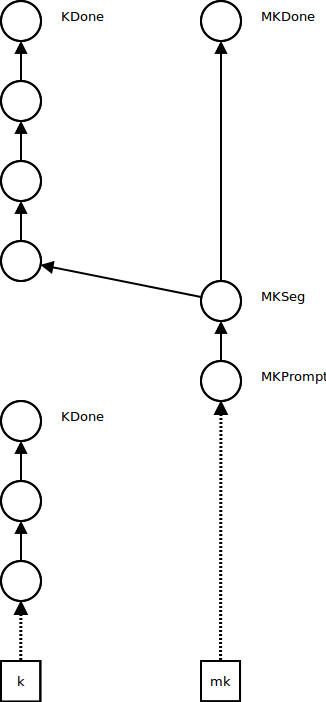
Further control operations push frames onto the metacontinuation, and create new empty continuations, as before:

When the ordinary continuation reaches KDone, we look at the metacontinuation: if it's MKDone, the program is finished and we return its result. Otherwise, we underflow the metacontinuation by reestablishing the next continuation segment as the current continuation and the next metacontinuation as the current metacontinuation.
An alternative API for continuations
Call/cc is the most well-known API for exposing first-class continuations to userland. But there is another API that's used in Scheme 48 and is also described in a paper by Feeley.
(continuation-capture f) --- calls f with the current continuation as argument. In contrast to call/cc, the continuation is not a procedure, but an opaque first-class object. (In Scheme 48, this is called primitive-cwcc.)
(continuation-graft k thunk) --- calls thunk in the continuation k. In contrast to call/cc, k doesn't receive a value computed in another continuation, but rather thunk's effect is performed in k. (Scheme 48: with-continuation.)
The implementation difference to call/cc is minimal, and expressing call/cc in terms of this API is simple:
I can't exactly put my finger on it, but this API seems more powerful than call/cc. In the implementation of delimited dynamic binding in terms of continuation marks I'm working on, there is a need for fetching the marks of another continuation. With call/cc this is impossible, but with this API I can prepend a thunk to the continuation in question, then in this thunk fetch the continuation's marks, and then jump out of it again.
(continuation-capture f) --- calls f with the current continuation as argument. In contrast to call/cc, the continuation is not a procedure, but an opaque first-class object. (In Scheme 48, this is called primitive-cwcc.)
(continuation-graft k thunk) --- calls thunk in the continuation k. In contrast to call/cc, k doesn't receive a value computed in another continuation, but rather thunk's effect is performed in k. (Scheme 48: with-continuation.)
The implementation difference to call/cc is minimal, and expressing call/cc in terms of this API is simple:
(define (call/cc f)
(continuation-capture
(lambda (k)
(f (lambda (val)
(continuation-graft k (lambda () val)))))))
I can't exactly put my finger on it, but this API seems more powerful than call/cc. In the implementation of delimited dynamic binding in terms of continuation marks I'm working on, there is a need for fetching the marks of another continuation. With call/cc this is impossible, but with this API I can prepend a thunk to the continuation in question, then in this thunk fetch the continuation's marks, and then jump out of it again.
Continuation marks
Continuation marks are a mechanism for attaching key-value data to continuation frames. There are two primitives:
(call/cm key value thunk) --- calls thunk with a new continuation mark binding key to value. If the current innermost continuation frame already has a mark with that key, it is overwritten.
(current-marks key) --- returns the list of values of current marks with the given key, from innermost to outermost continuation frame.
Example:
(call/cm 'foo 12 (lambda () (current-marks 'foo))) ---> (12)
So, continuation marks are an obvious mechanism for implementing dynamic binding. That duplicate marks on the same frame overwrite each other makes them play nice with TCO.
I've implemented CMs in the Kernel implementation I'm currently playing with. Every continuation frame has a marks dictionary mapping keys to values. Current-marks walks the continuation chain in the obvious way, collecting matching marks into a list. Call/cm clones the current continuation frame (including the marks dictionary) and updates the binding for the given key. I'm not entirely sure if that's the correct way to implement CMs, but it seems so.
I'm currently trying to implement delimited dynamic binding on top of continuation marks (using the metacontinuation approach from A Monadic Framework), but this seems slightly above my pay grade.
(call/cm key value thunk) --- calls thunk with a new continuation mark binding key to value. If the current innermost continuation frame already has a mark with that key, it is overwritten.
(current-marks key) --- returns the list of values of current marks with the given key, from innermost to outermost continuation frame.
Example:
(call/cm 'foo 12 (lambda () (current-marks 'foo))) ---> (12)
So, continuation marks are an obvious mechanism for implementing dynamic binding. That duplicate marks on the same frame overwrite each other makes them play nice with TCO.
I've implemented CMs in the Kernel implementation I'm currently playing with. Every continuation frame has a marks dictionary mapping keys to values. Current-marks walks the continuation chain in the obvious way, collecting matching marks into a list. Call/cm clones the current continuation frame (including the marks dictionary) and updates the binding for the given key. I'm not entirely sure if that's the correct way to implement CMs, but it seems so.
I'm currently trying to implement delimited dynamic binding on top of continuation marks (using the metacontinuation approach from A Monadic Framework), but this seems slightly above my pay grade.
Saturday, July 30, 2011
Some nice paperz on delimited continuations and first-class macros
My current obsessions are delimited continuations (see my intro post) and first-class macros (fexprs). Here are some nice papers related to these topics:
Three Implementation Models for Scheme is the dissertation of Kent Dybvig (of Chez Scheme fame). It contains a very nice abstract machine for (learning about) implementing a Scheme with first-class continuations. I'm currently trying to grok and implement this model, and then extend it to delimited continuations.
A Monadic Framework for Delimited Continuations contains probably the most succinct description of delimited continuations (on page 3), along with a typically hair-raising example of their use.
Adding Delimited and Composable Control to a Production Programming Environment. One of the authors is Matthew Flatt, so you know what to expect - a tour de force. The paper is about how Racket implements delimited control and integrates it with all the other features of Racket (dynamic-wind, exceptions, ...). Apropos, compared to Racket, Common Lisp is a lightweight language.
Fexprs as the basis of Lisp function application or $vau: the ultimate abstraction and the Revised-1 Report on the Kernel Programming Language. These two are probably the two papers I would take to the desert island at the moment. I'm only a long-time apprentice of programming languages, but I know genius when I see it.
Three Implementation Models for Scheme is the dissertation of Kent Dybvig (of Chez Scheme fame). It contains a very nice abstract machine for (learning about) implementing a Scheme with first-class continuations. I'm currently trying to grok and implement this model, and then extend it to delimited continuations.
A Monadic Framework for Delimited Continuations contains probably the most succinct description of delimited continuations (on page 3), along with a typically hair-raising example of their use.
Adding Delimited and Composable Control to a Production Programming Environment. One of the authors is Matthew Flatt, so you know what to expect - a tour de force. The paper is about how Racket implements delimited control and integrates it with all the other features of Racket (dynamic-wind, exceptions, ...). Apropos, compared to Racket, Common Lisp is a lightweight language.
Subcontinuations. This is an early paper on delimited continuations. It also describes control filters, a low level facility on top of which dynamic-wind can be implemented. Control filters are also mentioned - in passing - as a nice tool in the Racket paper (above).
If you know of any related nice papers, let me know!
On Twitter, Paul Snively mentioned Oleg's paper Delimited Control in OCaml, Abstractly and Concretely, but probably only because he's mentioned in the Acknowlegdements - kidding! It's a great paper, and I'm studying it too, but unfortunately it's not really applicable to implementing delimited control in JavaScript, which is what I'm trying to do.
Monday, April 26, 2010
Dylan and the Lisp family tree's central branch
Since the early eighties (beginning with Scheme and T), most Lisps began to settle around a common core.
(This also coincides with the point in time when static scoping was finally understood, once and for all, after a painful and embarrassing history.)
With the exception of Scheme, most Lisps don't have multi-shot continuations. They seriously complexify a language, as can be seen in weird implementation techniques like Cheney on the MTA.
It's also hard (or even impossible?) to make a good UNWIND-PROTECT in the face of multi-shot continuations. And UNWIND-PROTECT is surely one of the most important control flow operators.
So what is the common core I'm talking about? You can see it best in Dylan, I think.
First of all, a Lisp that follows this common core design can be efficiently implemented on real hardware. No need to do weird stuff like stack copying or Cheney on the MTA. In fact, Dylan has, with a bit of squinting, the same dynamic (control flow) semantics as C.
Second, the common core is simply nice to program in.
Some features of the common core:
All of them are great languages, and worth detailed study.
In the future I hope to write about each of the features these languages share in more detail.
(This also coincides with the point in time when static scoping was finally understood, once and for all, after a painful and embarrassing history.)
With the exception of Scheme, most Lisps don't have multi-shot continuations. They seriously complexify a language, as can be seen in weird implementation techniques like Cheney on the MTA.
It's also hard (or even impossible?) to make a good UNWIND-PROTECT in the face of multi-shot continuations. And UNWIND-PROTECT is surely one of the most important control flow operators.
So what is the common core I'm talking about? You can see it best in Dylan, I think.
First of all, a Lisp that follows this common core design can be efficiently implemented on real hardware. No need to do weird stuff like stack copying or Cheney on the MTA. In fact, Dylan has, with a bit of squinting, the same dynamic (control flow) semantics as C.
Second, the common core is simply nice to program in.
Some features of the common core:
- lexical exits
- unwind protection
- condition system with restarts
- global and lexical bindings
- first-class functions with optional, keyword, and rest parameters
- dynamic (thread-local) variables
- class-based object system
- generic functions
- powerful macros
- multiple return values
- semi-functional stateful programming style
All of them are great languages, and worth detailed study.
In the future I hope to write about each of the features these languages share in more detail.
Subscribe to:
Posts (Atom)
