Oleg's argument against call/cc links to one of his lesser known posts, Delimited continuations do dynamic-wind. In it he first shows how to implement yielding generators in terms of delimited control, and then shows how such generators lead to a natural definition of dynamic-wind, in userland, whereas with undelimited continuations, dynamic-wind has to be primitive.
(This is not entirely true. Kernel can implement dynamic-wind in userland, too, by means of its guarded undelimited continuations. And in Scheme 48, dynamic-wind is also implemented in userland with undelimited continuations, albeit in terms of a slightly lower level API than call/cc. Same is true for other Schemes, such as MIT Scheme. And probably the earliest definition of dynamic-wind, in Embedding Continuations in Procedural Objects is also in userland, so I'm a bit confused actually, as to why Oleg considers dynamic-wind primitive...)
Back to Oleg's generators in terms of delimited control. While one may argue against first-class continuations, whether delimited or not, I think having them in the language is great for quickly prototyping different ideas, such as generators. This has always been a forte of Lisp, and so high-powered control flow operations seem a good fit for the language, even if their runtime cost may be slightly higher than a more specialized, native implementation of some specific control feature, such as generators.
The basic ideas of generators are: you have a block of code, the generator, which may either normally return a value by means of reaching the end of the block, or it may intermittently yield a value. To call a generator, we need a boundary around it, so we wrap it in a prompt with reset. Yielding suspends the generator, capturing its delimited continuation up to the prompt, and delivers the value and this continuation to the caller, outside the boundary. Value and continuation are wrapped up in a special record type, so the caller can distinguish yields from an ordinary return, which doesn't wrap the value in any way (and neither provides a continuation for resuming, obviously). (This could probably be handled more elegantly with Racket's abort handlers.)
In this Gist, I've commented Oleg's implementation of generators and dynamic-wind.
I think it's a great example of how simple it is to add specific control flow features to a language with general (delimited) continuations.
Oh, and in typical Oleg style, the article then goes on about how you can implement call/cc in terms of generators, which makes his dynamic-wind compatible with existing Scheme examples using call/cc.
Showing posts with label delimited continuations. Show all posts
Showing posts with label delimited continuations. Show all posts
Saturday, August 11, 2012
Wednesday, August 1, 2012
Understanding metacontinuations for delimited control
Metacontinuations arise in some implementations of delimited control such as in A Monadic Framework for Delimited Continuations.
In addition to the usual continuation register K, an interpreter with metacontinuations has a metacontinuation register MK.
Initially, K points to an empty continuation KDone, and MK points to an empty metacontinuation MKDone:
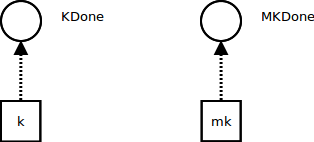
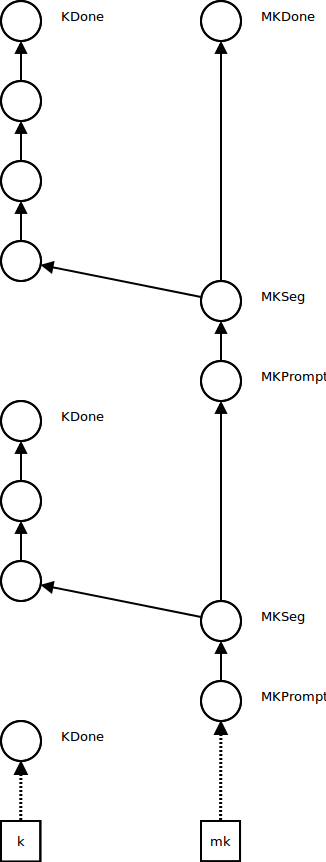
When the ordinary continuation reaches KDone, we look at the metacontinuation: if it's MKDone, the program is finished and we return its result. Otherwise, we underflow the metacontinuation by reestablishing the next continuation segment as the current continuation and the next metacontinuation as the current metacontinuation.
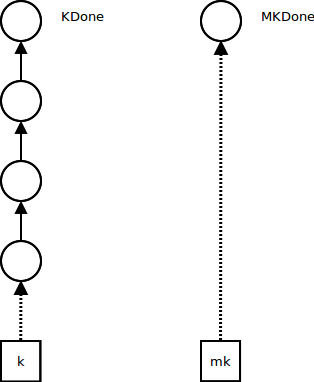
In addition to the usual continuation register K, an interpreter with metacontinuations has a metacontinuation register MK.
Initially, K points to an empty continuation KDone, and MK points to an empty metacontinuation MKDone:

Ordinary computations influence only the continuation K - they push continuation frames while the metacontinuation MK stays the same:

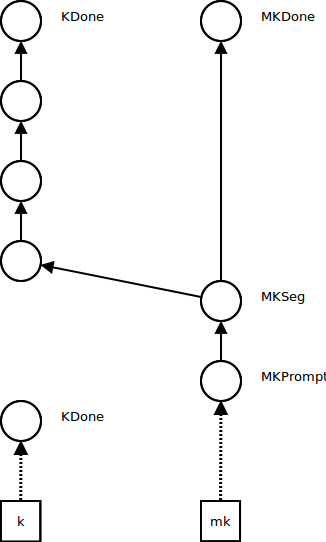
Control operations such as pushing a prompt (continuation delimiter) influence the metacontinuation. A segment metacontinuation frame MKSeg stores the continuation segment at which the control effect occurred and a pointer to the next metacontinuation. A prompt metacontinuation frame MKPrompt remembers the prompt and points to the segment frame (the reason for splitting this operation into two metacontinuation frames is that it makes the code simpler; see the paper). MK now points to the prompt metaframe, and K points to a new empty continuation KDone:

Further non-control computations occur in the new continuation, while the metacontinuation stays the same, as before:

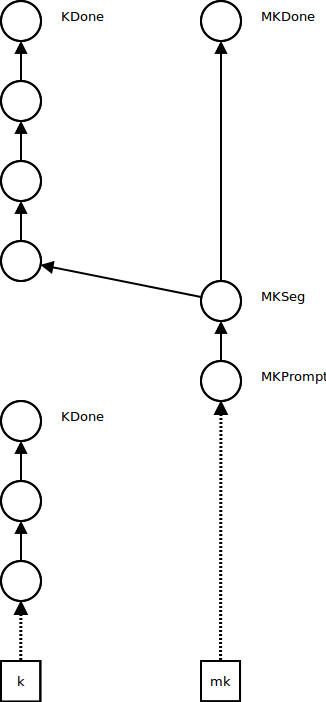
Further control operations push frames onto the metacontinuation, and create new empty continuations, as before:

When the ordinary continuation reaches KDone, we look at the metacontinuation: if it's MKDone, the program is finished and we return its result. Otherwise, we underflow the metacontinuation by reestablishing the next continuation segment as the current continuation and the next metacontinuation as the current metacontinuation.
Wednesday, July 18, 2012
Thursday, June 28, 2012
What I've been reading
If you want to impress your coworkers with terms like cobordism: Physics, Topology, Logic and Computation: A Rosetta Stone:
A simple diagram ... can now be seen as a quantum process, a tangle, a computation — or an abstract morphism in any braided monoidal category! This is just the sort of thing one would hope for in a general science of systems and processes.An Applicative Control-Flow Graph Based on Huet’s Zipper. Somebody actually used FP in the real world -- well, to write a compiler -- and can report that it did indeed in fact work. Related, here's my favorite zipper tutorial.
Resumable exceptions can macro-express delimited dynamic variables. Because you can never test your intuition enough.
More links: Ian Piumarta's liboop; Eric Torreborre on total FP; VeriML; automatic scoping and destructor functionality in C.
HT Paul Snively, Daniel Yokomizo, Patrick Thomson.
Thursday, August 18, 2011
Notes on delimited continuations
Delimited continuations are one of those topics where you need to spend months or maybe even years in the cloud of unknowing, until it suddenly makes click. At least, that's this autodidact's experience.
Delimited continuations are awesome, because they let us abstract over control flow - as I like to put it one man's control flow is another man's data, or as Chung-chieh Shan puts it: delimited continuations liberate control flow.
Continuations as we know them (i.e. those created by call/cc) are undelimited, they represent the whole rest of the computation. Delimited continuations represent the rest of a sub-computation up to a given prompt. They come from investigating REPLs: when you capture an undelimited continuation, the continuation includes the REPL's control flow! Generally, you don't want that, so with delimited continuations, the REPL can install a prompt before executing code entered by the user, and then you can capture a delimited continuation just up to that prompt, excluding the REPL's code.
My favorite description of delimited continuations is offered right at the start of A Monadic Framework for Delimited Continuations, even though the rest of the paper is quite over my head. Their API for delimited continuations is:
- newPrompt --- creates a fresh prompt, distinct from all other prompts. It's just an object that we use as an identifier, basically. Some systems simply use symbols for prompts.
- pushPrompt p e --- pushes prompt p on the stack, and executes expression e in this new context. This delimits the stack, so we can later capture a delimited continuation up to this part of the stack.
- withSubCont p f --- aborts (unwinds the stack) up to and including the prompt p, and calls the function f with a single argument k representing the delimited continuation from the call to withSubCont up to but not including the prompt. This captures a delimited continuation, analogous to how call/cc captures an undelimited continuation.
- pushSubCont k e --- pushes the delimited continuation k on the stack, and executes expression e in this new context. This composes the stack of k with the current stack, analogous to how calling the function representing a continuation in Scheme swaps the current stack with the stack of that continuation.
Now to the example! Delimited continuation examples are always hair-raising!! Brace yourself!!!
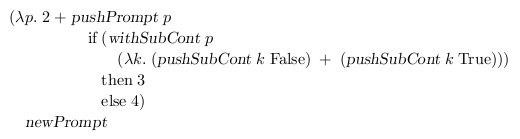
So, the first thing we do is call newPrompt (at the bottom) to obtain a fresh prompt, and then we pipe that into the function (at the top), so that we have a name, p, for the prompt. Inside that function we have the addition of 2 to a second expression, that pushPrompt's p on the stack, i.e. delimits the stack at this point. The if is called inside the new context delimited by p. Now it gets hairy: The if's test expression is a withSubCont, so it immediately aborts up to the outer pushPrompt and then calls the function that is its second argument with k bound to the rest of the computation between the withSubCont and the pushPrompt. What's the rest of that computation?? Well, by the magic of delimited control, k is now equivalent to the function λb. if b then 3 else 4. This is what I meant when I said that delimited continuations allow us to abstract over control flow - we have just turned an arbitrary, dynamic control flow sequence into a function. (Well, it's not really a function, but we can use it like one.) OK, so we have aborted back up to pushPrompt, and in k we have the rest of the computation as a function. What do we do with it? Well, we call it using pushSubCont once with False and once with True as argument, and we add the two results, giving us 7. Note that we just called the delimited continuation twice! We can not only abstract over arbitrary control flows, we can also call them as many times as we like. Now the whole shebang inside pushPrompt is over, and we return to the addition of 2 to our result of 7, giving us 9.
Previously: papers on delimited continuations.
Subscribe to:
Posts (Atom)


