Friday, November 9, 2012
Thursday, November 8, 2012
Monday, November 5, 2012
Sunday, November 4, 2012
Thursday, September 27, 2012
Wednesday, September 19, 2012
Saturday, September 8, 2012
Having both fexprs and macros
Lexically-scoped fexprs and first-class environments make it simple to do hygienic metaprogramming, using less machinery than hygienic macro systems, and they also require less concepts in the language: there is no need to specify a preprocessing phase.
The downside is that fexprs always incur an interpretative overhead with current technology. Many are convinced that those fexprs that do similar things to what macros do can be partially evaluated: "my research in static analysis leads me to believe that we will be able to erase that overhead for the common case--where first-class macros are used to do the job of compile-time macros" writes Matt Might, for example.
In my new language, Wat, I've implemented both fexprs and macros. Macros are expanded at runtime, when they are first encountered, and their result is memoized in the syntax tree, a technique described in two interesting articles (1, 2) related to the SCM Scheme implementation.
In Wat, MACRO is a special form that can be wrapped around a combiner, and causes calls to that combiner to be memoized in the source tree. An example, LET:
Macros complicate the language quite a bit; but used in moderation, especially for forms like LET that are basically never changed nor used in a higher-order fashion, they should be unproblematic, and offer a nice speed boost. Fexprs should be used for more complex tasks that require special attention to hygiene, or need to do things that macros can't do, whereas macros could be used for simple transformation and processing tasks, such as UNTIL, above.
Oh, and it should also be noted that these macros enjoy a nice level of hygiene already, by virtue of first-class environments and first-class combiners. For example, UNTIL above doesn't insert the symbols WHILE or NOT into the generated code - it inserts the actual values, therefore being protected from variable shadowing by calling code.
The downside is that fexprs always incur an interpretative overhead with current technology. Many are convinced that those fexprs that do similar things to what macros do can be partially evaluated: "my research in static analysis leads me to believe that we will be able to erase that overhead for the common case--where first-class macros are used to do the job of compile-time macros" writes Matt Might, for example.
In my new language, Wat, I've implemented both fexprs and macros. Macros are expanded at runtime, when they are first encountered, and their result is memoized in the syntax tree, a technique described in two interesting articles (1, 2) related to the SCM Scheme implementation.
In Wat, MACRO is a special form that can be wrapped around a combiner, and causes calls to that combiner to be memoized in the source tree. An example, LET:
(def let
(macro (vau (bindings . body) #ign
(cons (list* lambda (map car bindings) body)
(map cadr bindings)))))
With a bit of sugar, one can write macros that look almost like in Common Lisp:
(define-macro (until test . body) (list* while (list not test) body))
Macros complicate the language quite a bit; but used in moderation, especially for forms like LET that are basically never changed nor used in a higher-order fashion, they should be unproblematic, and offer a nice speed boost. Fexprs should be used for more complex tasks that require special attention to hygiene, or need to do things that macros can't do, whereas macros could be used for simple transformation and processing tasks, such as UNTIL, above.
Oh, and it should also be noted that these macros enjoy a nice level of hygiene already, by virtue of first-class environments and first-class combiners. For example, UNTIL above doesn't insert the symbols WHILE or NOT into the generated code - it inserts the actual values, therefore being protected from variable shadowing by calling code.
Thursday, September 6, 2012
Mixing first-order and higher-order control
It's desirable for a language to support exceptions (preferably restartable ones), unwind protection, dynamic binding, and delimited continuations. [Adding Delimited and Composable Control to a Production Programming Environment, Delimited Dynamic Binding]
I've found a tractable way to implement these features in the language I'm currently working on, Wat.
My approach is to totally separate first-order control from higher-order control.
There is a set of Common Lisp-like first-order forms:
Restartable exceptions are implemented in terms of these first-order forms and dynamically-bound variables, which are also provided natively.
In addition there's a completely separate set of higher-order control forms from A Monadic Framework for Delimited Continuations.
Delimited continuations are implemented using a technique similar to Exceptional Continuations: ordinary code paths run on the normal JS stack; when a continuation is captured, the stack is unwound frame by frame up to the prompt, and at each frame, a resumption is added to the continuation that is built up during the unwinding. This technique is ten times faster than a naive scheme with heap-allocated stack frames, but currently doesn't support TCO.
First-order control is used for quotidian control flow, whereas higher-order control is used for heavy control flow lifting, such as making a REPL written in direct style work in the browser's asynchronous environment.
This is a quite intuitive model: in the small, one has the usual Common Lisp control flow, including restartable exceptions, whereas in the large, behind the scenes, control flow may be arbitrarily abstracted and composed with the higher-order control forms.
I've found a tractable way to implement these features in the language I'm currently working on, Wat.
My approach is to totally separate first-order control from higher-order control.
There is a set of Common Lisp-like first-order forms:
- block and return-from that establish and invoke a lexically-scoped one-shot escape continuation, respectively.
- unwind-protect aka "finally". Notably, unwind-protect is only sensitive to return-from, not to aborts via higher-order control.
These forms are implemented natively using JS try/catch and finally.
In addition there's a completely separate set of higher-order control forms from A Monadic Framework for Delimited Continuations.
Delimited continuations are implemented using a technique similar to Exceptional Continuations: ordinary code paths run on the normal JS stack; when a continuation is captured, the stack is unwound frame by frame up to the prompt, and at each frame, a resumption is added to the continuation that is built up during the unwinding. This technique is ten times faster than a naive scheme with heap-allocated stack frames, but currently doesn't support TCO.
First-order control is used for quotidian control flow, whereas higher-order control is used for heavy control flow lifting, such as making a REPL written in direct style work in the browser's asynchronous environment.
This is a quite intuitive model: in the small, one has the usual Common Lisp control flow, including restartable exceptions, whereas in the large, behind the scenes, control flow may be arbitrarily abstracted and composed with the higher-order control forms.
Wednesday, September 5, 2012
Reactive Demand Programming
David Barbour has created a very promising and exciting paradigm for writing interactive, networked applications: Reactive Demand Programming (RDP).
RDP is very sophisticated and I can't really do it justice here, but its salient points are:
RDP is very sophisticated and I can't really do it justice here, but its salient points are:
- An RDP application is a dynamically-changing set of semi-permanent, bidirectional data exchanges, called behaviors. What pipes are to Unix, behaviors are to RDP.
- A signal is a monodirectional channel carrying a value, and varies discretely over time.
- A behavior is made up of one or more input signals, called demands, and a single output signal.
- RDP builds in the notion of anticipation - every signal update comes with the expected duration the new value is valid. This allows low latency through smart scheduling.
- [Update: See David's corrections in the comments.]
An example for a behavior would be a camera receiving move and zoom commands (or rather demands) with discrete time intervals (e.g. as long as a user moves the camera joystick) from one or more users on input signals, interpolating these commands using some deterministic decision procedure (such as averaging all commands), and outputting camera frames on the output signal, with the anticipation measure telling clients something about the rate at which the camera refreshes, allowing them to smartly perform display reprocessing.
The best way to get started is the README of David's RDP implementation. David has also just posted a progress report on his blog, which contains many articles on RDP.
I think RDP is one of the most exciting developments in interactive application development and is worth checking out.
Thursday, August 23, 2012
Tuesday, August 14, 2012
Switching between TCO and non-TCO at runtime
Here's a fun idea, that should work in a language with fexprs, or an incremental/reactive macro expander. It relies on the property that EVAL evaluates the form in tail position. Tail-call optimization could be switched off and on during debugging for more useful stack traces, and even arbitrarily at runtime. The loss of useful stacktraces is not a non-issue, as witnessed by attempts at more useful stack traces in MIT Scheme and in SISC.
How it works: all expressions in tail position (e.g. the last expression of a BEGIN, the last expression in a lambda, the branches of an IF, ...) are automatically (by the parser or something) wrapped in a call to the operator TCOIFY:
(lambda () (foo) (bar)) becomes
(lambda () (foo) (tcoify (bar)))
(if (quux) (do-something) (do-something-else)) becomes
(if (quux) (tcoify (do-something)) (tcoify (do-something-else)))
etc.
Ordinarily, TCOIFY would be a fexpr that directly evaluates its argument, in tail position:
(def tcoify (vau (x) env (eval x env)))
When TCOIFY is defined thusly, (tcoify expr) is equal to expr for the purposes of TCO, because EVAL evaluates X in tail position.
For useful stack traces, one would define TCOIFY as a function. Argument evaluation needs to happen before application, so TCOIFY would prevent TCO:
(def tcoify (lambda (x) x))
By switching between the two definitions of TCOIFY at runtime, tail-call optimization can be turned on and off.
How it works: all expressions in tail position (e.g. the last expression of a BEGIN, the last expression in a lambda, the branches of an IF, ...) are automatically (by the parser or something) wrapped in a call to the operator TCOIFY:
(lambda () (foo) (bar)) becomes
(lambda () (foo) (tcoify (bar)))
(if (quux) (do-something) (do-something-else)) becomes
(if (quux) (tcoify (do-something)) (tcoify (do-something-else)))
etc.
Ordinarily, TCOIFY would be a fexpr that directly evaluates its argument, in tail position:
(def tcoify (vau (x) env (eval x env)))
When TCOIFY is defined thusly, (tcoify expr) is equal to expr for the purposes of TCO, because EVAL evaluates X in tail position.
For useful stack traces, one would define TCOIFY as a function. Argument evaluation needs to happen before application, so TCOIFY would prevent TCO:
(def tcoify (lambda (x) x))
By switching between the two definitions of TCOIFY at runtime, tail-call optimization can be turned on and off.
Saturday, August 11, 2012
Delimited continuations do dynamic-wind
Oleg's argument against call/cc links to one of his lesser known posts, Delimited continuations do dynamic-wind. In it he first shows how to implement yielding generators in terms of delimited control, and then shows how such generators lead to a natural definition of dynamic-wind, in userland, whereas with undelimited continuations, dynamic-wind has to be primitive.
(This is not entirely true. Kernel can implement dynamic-wind in userland, too, by means of its guarded undelimited continuations. And in Scheme 48, dynamic-wind is also implemented in userland with undelimited continuations, albeit in terms of a slightly lower level API than call/cc. Same is true for other Schemes, such as MIT Scheme. And probably the earliest definition of dynamic-wind, in Embedding Continuations in Procedural Objects is also in userland, so I'm a bit confused actually, as to why Oleg considers dynamic-wind primitive...)
Back to Oleg's generators in terms of delimited control. While one may argue against first-class continuations, whether delimited or not, I think having them in the language is great for quickly prototyping different ideas, such as generators. This has always been a forte of Lisp, and so high-powered control flow operations seem a good fit for the language, even if their runtime cost may be slightly higher than a more specialized, native implementation of some specific control feature, such as generators.
The basic ideas of generators are: you have a block of code, the generator, which may either normally return a value by means of reaching the end of the block, or it may intermittently yield a value. To call a generator, we need a boundary around it, so we wrap it in a prompt with reset. Yielding suspends the generator, capturing its delimited continuation up to the prompt, and delivers the value and this continuation to the caller, outside the boundary. Value and continuation are wrapped up in a special record type, so the caller can distinguish yields from an ordinary return, which doesn't wrap the value in any way (and neither provides a continuation for resuming, obviously). (This could probably be handled more elegantly with Racket's abort handlers.)
In this Gist, I've commented Oleg's implementation of generators and dynamic-wind.
I think it's a great example of how simple it is to add specific control flow features to a language with general (delimited) continuations.
Oh, and in typical Oleg style, the article then goes on about how you can implement call/cc in terms of generators, which makes his dynamic-wind compatible with existing Scheme examples using call/cc.
(This is not entirely true. Kernel can implement dynamic-wind in userland, too, by means of its guarded undelimited continuations. And in Scheme 48, dynamic-wind is also implemented in userland with undelimited continuations, albeit in terms of a slightly lower level API than call/cc. Same is true for other Schemes, such as MIT Scheme. And probably the earliest definition of dynamic-wind, in Embedding Continuations in Procedural Objects is also in userland, so I'm a bit confused actually, as to why Oleg considers dynamic-wind primitive...)
Back to Oleg's generators in terms of delimited control. While one may argue against first-class continuations, whether delimited or not, I think having them in the language is great for quickly prototyping different ideas, such as generators. This has always been a forte of Lisp, and so high-powered control flow operations seem a good fit for the language, even if their runtime cost may be slightly higher than a more specialized, native implementation of some specific control feature, such as generators.
The basic ideas of generators are: you have a block of code, the generator, which may either normally return a value by means of reaching the end of the block, or it may intermittently yield a value. To call a generator, we need a boundary around it, so we wrap it in a prompt with reset. Yielding suspends the generator, capturing its delimited continuation up to the prompt, and delivers the value and this continuation to the caller, outside the boundary. Value and continuation are wrapped up in a special record type, so the caller can distinguish yields from an ordinary return, which doesn't wrap the value in any way (and neither provides a continuation for resuming, obviously). (This could probably be handled more elegantly with Racket's abort handlers.)
In this Gist, I've commented Oleg's implementation of generators and dynamic-wind.
I think it's a great example of how simple it is to add specific control flow features to a language with general (delimited) continuations.
Oh, and in typical Oleg style, the article then goes on about how you can implement call/cc in terms of generators, which makes his dynamic-wind compatible with existing Scheme examples using call/cc.
Tuesday, August 7, 2012
Scheme's missing ingredient: first-class type tags
I've always felt that Scheme does data and types wrong, but I couldn't really say what bothered me until yesterday. After all, R7RS now has define-record-type for creating disjoint types. But that ain't enuff!
In my new language, Wat, I've found a satisfying solution, inspired by Kernel's encapsulation types, but going beyond them slightly. There are two procedures:
In my new language, Wat, I've found a satisfying solution, inspired by Kernel's encapsulation types, but going beyond them slightly. There are two procedures:
- (make-type) returns a list of three elements: 1) a first-class type 2) a tagger function for tagging a value with that type, creating a tagged object and 3) an untagger function for extracting the value of tagged objects of that type.
- (type-of obj) returns the first-class type of an object. The crucial point is that type-of not only works for tagged objects of user-defined types created by make-type, but also for all built-in types. E.g. (type-of 12) will return the number first-class type.
This system has the benefits of Kernel's encapsulated types: only someone with access to the tagger function (capability) may create new instances of a type. Only someone with access to the untagger function may access the contents of tagged objects. So object contents are potentially fully encapsulated.
But at the same time, the fact that every object, including built-in ones, has a first-class type makes it possible to efficiently program generically. E.g. one may create Smalltalk-like dynamic dispatch by using the first-class types of objects as indexes into a virtual lookup table of a generic function. This is not possible in either Scheme or Kernel. In both languages, programming generically requires one to use a cascade of type predicates (e.g. number?).
Example in Wat:
Example in Wat:
; destructuringly bind the three elements ; returned by make-type (def (person-type person-tagger person-untagger) (make-type)) (define (make-person name email) (person-tagger (list name email))) ; untagger also performs a type check that ; person is in fact of type person (define (get-name person) (car (person-untagger person))) (define (get-email person) (cadr (person-untagger person))) (define p1 (make-person "Quux" "quux@example.com")) (get-name p1) --> "Quux" (get-email p1) --> "quux@example.com"
Thursday, August 2, 2012
Wednesday, August 1, 2012
Understanding metacontinuations for delimited control
Metacontinuations arise in some implementations of delimited control such as in A Monadic Framework for Delimited Continuations.
In addition to the usual continuation register K, an interpreter with metacontinuations has a metacontinuation register MK.
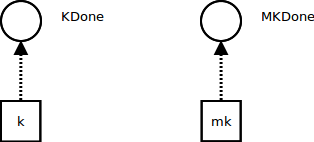
Initially, K points to an empty continuation KDone, and MK points to an empty metacontinuation MKDone:
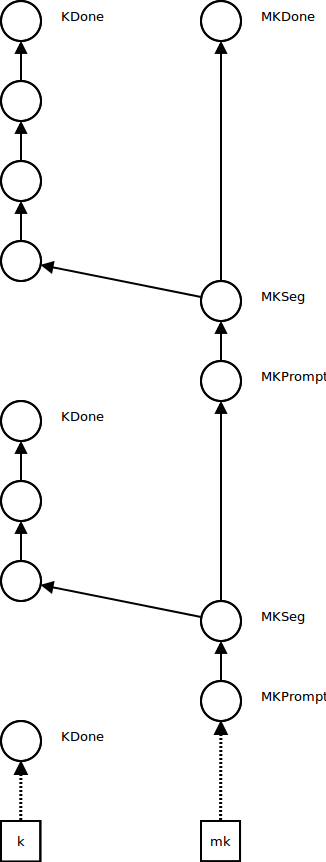
When the ordinary continuation reaches KDone, we look at the metacontinuation: if it's MKDone, the program is finished and we return its result. Otherwise, we underflow the metacontinuation by reestablishing the next continuation segment as the current continuation and the next metacontinuation as the current metacontinuation.
In addition to the usual continuation register K, an interpreter with metacontinuations has a metacontinuation register MK.
Initially, K points to an empty continuation KDone, and MK points to an empty metacontinuation MKDone:

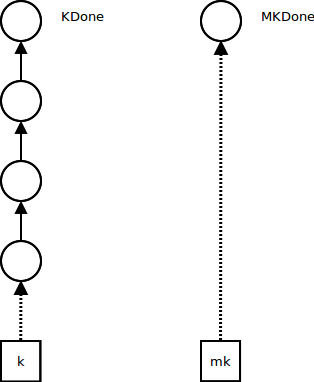
Ordinary computations influence only the continuation K - they push continuation frames while the metacontinuation MK stays the same:

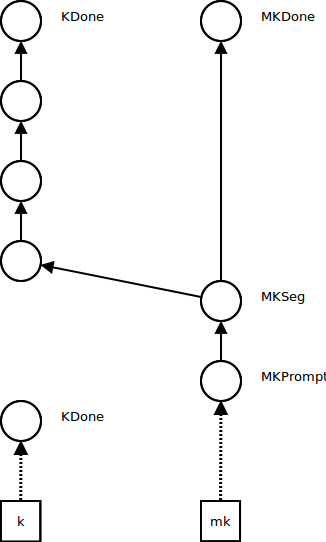
Control operations such as pushing a prompt (continuation delimiter) influence the metacontinuation. A segment metacontinuation frame MKSeg stores the continuation segment at which the control effect occurred and a pointer to the next metacontinuation. A prompt metacontinuation frame MKPrompt remembers the prompt and points to the segment frame (the reason for splitting this operation into two metacontinuation frames is that it makes the code simpler; see the paper). MK now points to the prompt metaframe, and K points to a new empty continuation KDone:

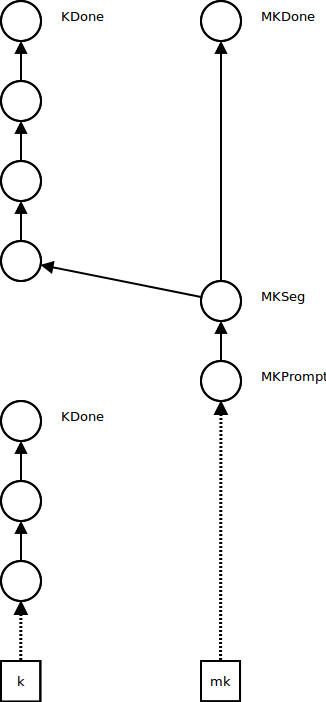
Further non-control computations occur in the new continuation, while the metacontinuation stays the same, as before:

Further control operations push frames onto the metacontinuation, and create new empty continuations, as before:

When the ordinary continuation reaches KDone, we look at the metacontinuation: if it's MKDone, the program is finished and we return its result. Otherwise, we underflow the metacontinuation by reestablishing the next continuation segment as the current continuation and the next metacontinuation as the current metacontinuation.
An alternative API for continuations
Call/cc is the most well-known API for exposing first-class continuations to userland. But there is another API that's used in Scheme 48 and is also described in a paper by Feeley.
(continuation-capture f) --- calls f with the current continuation as argument. In contrast to call/cc, the continuation is not a procedure, but an opaque first-class object. (In Scheme 48, this is called primitive-cwcc.)
(continuation-graft k thunk) --- calls thunk in the continuation k. In contrast to call/cc, k doesn't receive a value computed in another continuation, but rather thunk's effect is performed in k. (Scheme 48: with-continuation.)
The implementation difference to call/cc is minimal, and expressing call/cc in terms of this API is simple:
I can't exactly put my finger on it, but this API seems more powerful than call/cc. In the implementation of delimited dynamic binding in terms of continuation marks I'm working on, there is a need for fetching the marks of another continuation. With call/cc this is impossible, but with this API I can prepend a thunk to the continuation in question, then in this thunk fetch the continuation's marks, and then jump out of it again.
(continuation-capture f) --- calls f with the current continuation as argument. In contrast to call/cc, the continuation is not a procedure, but an opaque first-class object. (In Scheme 48, this is called primitive-cwcc.)
(continuation-graft k thunk) --- calls thunk in the continuation k. In contrast to call/cc, k doesn't receive a value computed in another continuation, but rather thunk's effect is performed in k. (Scheme 48: with-continuation.)
The implementation difference to call/cc is minimal, and expressing call/cc in terms of this API is simple:
(define (call/cc f)
(continuation-capture
(lambda (k)
(f (lambda (val)
(continuation-graft k (lambda () val)))))))
I can't exactly put my finger on it, but this API seems more powerful than call/cc. In the implementation of delimited dynamic binding in terms of continuation marks I'm working on, there is a need for fetching the marks of another continuation. With call/cc this is impossible, but with this API I can prepend a thunk to the continuation in question, then in this thunk fetch the continuation's marks, and then jump out of it again.
Continuation marks
Continuation marks are a mechanism for attaching key-value data to continuation frames. There are two primitives:
(call/cm key value thunk) --- calls thunk with a new continuation mark binding key to value. If the current innermost continuation frame already has a mark with that key, it is overwritten.
(current-marks key) --- returns the list of values of current marks with the given key, from innermost to outermost continuation frame.
Example:
(call/cm 'foo 12 (lambda () (current-marks 'foo))) ---> (12)
So, continuation marks are an obvious mechanism for implementing dynamic binding. That duplicate marks on the same frame overwrite each other makes them play nice with TCO.
I've implemented CMs in the Kernel implementation I'm currently playing with. Every continuation frame has a marks dictionary mapping keys to values. Current-marks walks the continuation chain in the obvious way, collecting matching marks into a list. Call/cm clones the current continuation frame (including the marks dictionary) and updates the binding for the given key. I'm not entirely sure if that's the correct way to implement CMs, but it seems so.
I'm currently trying to implement delimited dynamic binding on top of continuation marks (using the metacontinuation approach from A Monadic Framework), but this seems slightly above my pay grade.
(call/cm key value thunk) --- calls thunk with a new continuation mark binding key to value. If the current innermost continuation frame already has a mark with that key, it is overwritten.
(current-marks key) --- returns the list of values of current marks with the given key, from innermost to outermost continuation frame.
Example:
(call/cm 'foo 12 (lambda () (current-marks 'foo))) ---> (12)
So, continuation marks are an obvious mechanism for implementing dynamic binding. That duplicate marks on the same frame overwrite each other makes them play nice with TCO.
I've implemented CMs in the Kernel implementation I'm currently playing with. Every continuation frame has a marks dictionary mapping keys to values. Current-marks walks the continuation chain in the obvious way, collecting matching marks into a list. Call/cm clones the current continuation frame (including the marks dictionary) and updates the binding for the given key. I'm not entirely sure if that's the correct way to implement CMs, but it seems so.
I'm currently trying to implement delimited dynamic binding on top of continuation marks (using the metacontinuation approach from A Monadic Framework), but this seems slightly above my pay grade.
Thursday, July 26, 2012
Subscribe to:
Posts (Atom)














